Let’s consider a scenario - you have different set of tasks and all of those tasks have got a priority attached to it.
All you want to know is what is the next task with highest priority which you need to pick.
Lets say you have n tasks. One way to know which task carries the most priority is to sort them, right ?
So, if we do sort them, the time complexity of the sorting process will be O(nlogn).
Now, after spending O(nlogn) time, what if we need to add a new task with a new priority to the set ? We’ll have to spend another O(n) time complexity to put the task in its rightful place in the sorted array.
Is there any other faster way to achieve this ? Yes, Heaps.
Heap Property
Heap is nothing but a tree of nodes which adheres to one fixed property, which is - the value of the parent of any of the nodes should be less than OR greater than the values of its children.
If the value of the parent node < the values of its children - Its a Min Heap.
If the value of the parent node > the values of its children - Its a Max Heap.
Binary Heap
There are many ways heaps can be constructed, but the most common form of heaps are binary heaps which have got some special characteristics -
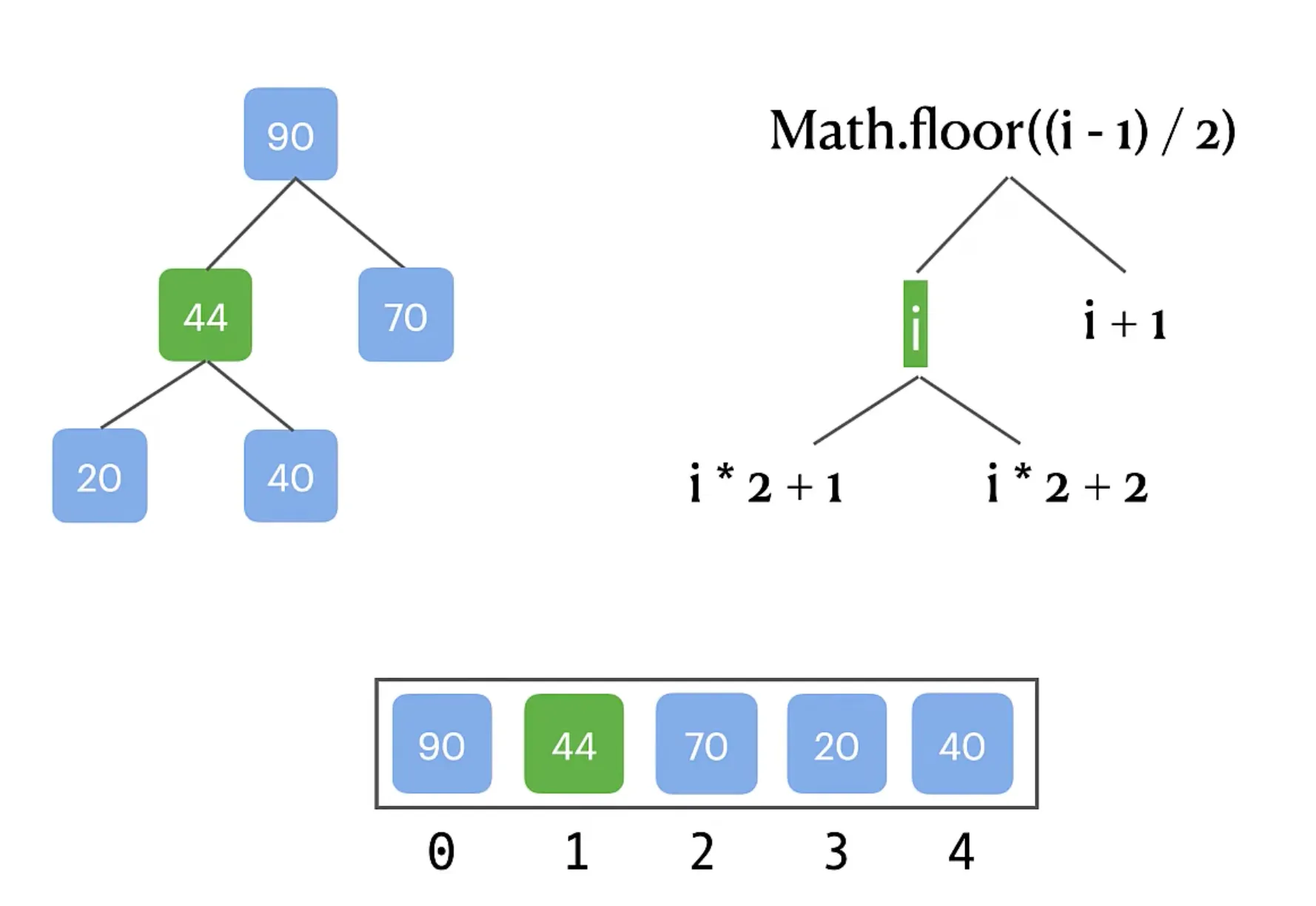
- Its a completed binary tree, which means - each node can have 2 children only, and all rows are filled, except maybe the last one, wherein values are filled from the left.
- It can be represented via an array.
- Position of the children and parent of a node in this array can be easily calculated.
Lets do a bit of coding as well alongside, shall we ?
We’ll be using a JavaScript class to implement a Binary Heap.
class MinHeap {
constructor() {
this.data = [];
}
// ...
// ...
}
Calculations
Parent of node at index i - Math.floor((i - 1)/2)
Left child of node at index i - 2*i + 1
Right child of node at index i - 2*i + 2
Lets implement methods in our class to obtain the above indices -
getLeftChildIndex(i) {
return 2 * i + 1;
}
getRightChildIndex(i) {
return 2 * i + 2;
}
getParentIndex(i) {
return Math.floor((i - 1)/2);
}
Push operation
This is the insertion operation. Whenever a new item or a task or a node is inserted into a min/max binary heap -
- The new item is added at the end of the array.
- Then, since we now need to make sure that heap property is still intact - we heapify up.
push(key) {
// pushing the key onto the heap
// first we push it to the last element
this.data.push(key);
// then we heapify up
this.heapifyUp();
}
What is heapifying up ?
Considering we are implementing a Min Heap, starting from the recently inserted element, we need to recursively check whether the parent node contains a value which is less than its children or not.
If it is not - swap values at both places.
heapifyUp() {
// we will start with last index
let currentIndex = this.data.length - 1;
while (this.data[currentIndex] < this.data[this.getParentIndex(currentIndex)]) {
this.swap(currentIndex, this.getParentIndex(currentIndex));
currentIndex = this.getParentIndex(currentIndex);
}
}
We keep doing this until parent node is reached.
Poll operation
Polling in a heap means taking out the root node from the tree which will always be either the minimum value or the maximum value of all the elements in the data structure depending on whether its a min heap or a max heap.
Once root node is taken out of the tree -
- We put the last element of the array/tree in its place.
- Then, since we now need to make sure that heap property is still intact - we heapify down.
poll() {
// when we poll we remove the head, and replace it with the last element of the heap
const polledValue = this.data[0];
this.data[0] = this.data[this.data.length - 1];
// now remove the last element
this.data.length--;
// then we heapify down
this.heapifyDown();
return polledValue;
}
What is heapifying down ?
Considering we are implementing a Min Heap, starting from the newly appointed root node, we need to recursively check whether the parent node contains a value which is less than its children or not.
If it is not - swap values at both places.
heapifyDown() {
// we need to start from the top
let currentIndex = 0;
// we need to move down till there are no children present
// Left child always gets populated first in a completed binary tree
while (this.getLeftChildIndex(currentIndex) !== undefined) {
// now we need to find the minimum of the 2 children
let minChildIndex = this.getLeftChildIndex(currentIndex);
if (this.getRightChildIndex(currentIndex) !== undefined && this.data[this.getRightChildIndex(currentIndex)] < this.data[this.getLeftChildIndex(currentIndex)]) {
// right child exists and is less than the left child
minChildIndex = this.getRightChildIndex(currentIndex);
}
// we need to swap if val at currentIndex > val at minChildIndex
if (this.data[currentIndex] > this.data[minChildIndex]) {
this.swap(currentIndex, minChildIndex);
currentIndex = minChildIndex;
} else {
// the parent is already smaller than its children
return;
}
}
}
We keep doing this until leaf node is reached, or when there is no need to swap again.
Time taken by Heaps
Lets get straight to the numbers. Time complexity of -
- Push operation -
O(logn) - Poll operation -
O(logn) - Building a binary heap -
O(nlogn)as creating a heap ofnelements mean pushingnelements one-by-one.
You have to agree, this is much more faster, and also enough to impress interviewers.
Leetcode questions
Look out for problems which want you to find Top K elements. You’ll probably need a min/max heap here. Some leetcode problems that you can practice heaps with -
- 215 Kth Largest Element in an Array
- 347 Top K Frequent Elements
- 373 Find K Pairs With Smallest Sums
All stitched together
Here is a complete code for implementing a Min Heap.
class MinHeap {
constructor() {
this.data = [];
}
getLeftChildIndex(i) {
return 2 * i + 1;
}
getRightChildIndex(i) {
return 2 * i + 2;
}
getParentIndex(i) {
return Math.floor((i - 1)/2);
}
swap(i1, i2) {
// swapping 2 indices
let temp = this.data[i1];
this.data[i1] = this.data[i2];
this.data[i2] = temp;
}
heapifyUp() {
// we will start with last index
let currentIndex = this.data.length - 1;
while (this.data[currentIndex] < this.data[this.getParentIndex(currentIndex)]) {
this.swap(currentIndex, this.getParentIndex(currentIndex));
currentIndex = this.getParentIndex(currentIndex);
}
}
heapifyDown() {
// we need to start from the top
let currentIndex = 0;
// we need to move down till there are no children present
// Left child always gets populated first in a completed binary tree
while (this.getLeftChildIndex(currentIndex) !== undefined) {
// now we need to find the minimum of the 2 children
let minChildIndex = this.getLeftChildIndex(currentIndex);
if (this.getRightChildIndex(currentIndex) !== undefined && this.data[this.getRightChildIndex(currentIndex)] < this.data[this.getLeftChildIndex(currentIndex)]) {
// right child exists and is less than the left child
minChildIndex = this.getRightChildIndex(currentIndex);
}
// we need to swap if val at currentIndex > val at minChildIndex
if (this.data[currentIndex] > this.data[minChildIndex]) {
this.swap(currentIndex, minChildIndex);
currentIndex = minChildIndex;
} else {
// the parent is already smaller than its children
return;
}
}
}
push(key) {
// pushing the key onto the heap
// first we push it to the last element
this.data.push(key);
// then we heapify up
this.heapifyUp();
}
poll() {
// when we poll we remove the head, and replace it with the last element of the heap
const polledValue = this.data[0];
this.data[0] = this.data[this.data.length - 1];
// now remove the last element
this.data.length--;
// then we heapify down
this.heapifyDown();
return polledValue;
}
}
