Today, we’ll be looking at 2 of the most famous algorithms of all time - Breadth First Search (BFS) and Depth First Search (DFS), and how we can use them to traverse graphs.

Lets first look at what a graph is and how we can represent them.

Graphs and Adjacency List

Graphs are data structures that represent data using vertices (nodes) connected via edges. And how can we represent graphs in code ?

We can use an Adjacency list which is just a 2-D array containing neighbors of the nodes such that ith entry of the array contains neighbors of node i.

Lets look at an example of a graph and an adjacency list on which we will be applying BFS and DFS.

So a graph which has got an adjacency list -

[[1, 2], [0, 2, 3], [0, 1, 4], [1, 4], [2, 3, 5], [4, 6], [5]]

will look something like -

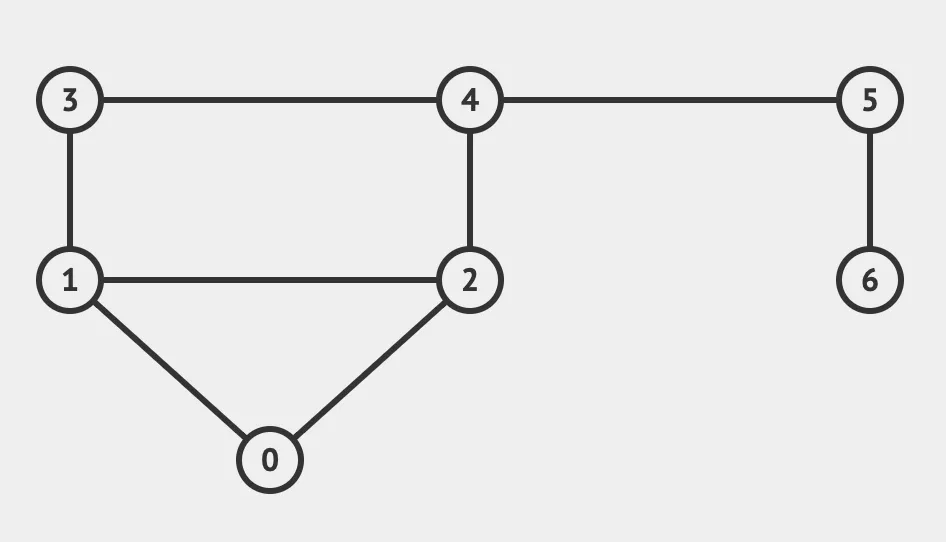
We’ll be feeding the adjacency list to our algorithms later. Lets take a look at them now.

Depth First Search (DFS)

With DFS, we start at a source node and explore as far as possible along each branch before backtracking.

This can be done iteratively through stack data structure but the most popular implementation of DFS is via recursion.

function dfs(adj: number[][], node: number, visited: boolean[]) {
    visited[node] = true;
    console.log(node);
    
    for (let i of adj[node]) {
        if (!visited[i]) dfs(adj, i, visited);
    }
}

As you can see, we have maintained a boolean array visited because we want to make sure we are not visiting the same node twice.

If I feed the adjacency list we saw above, we will get this output -

const adjList = [[1, 2], [0, 2, 3], [0, 1, 4], [1, 4], [2, 3, 5], [4, 6], [5]];
const visited = new Array(adjList.length).fill(false);
dfs(adjList, 0, visited); // 0 1 2 4 3 5 6

Uses

It can be used to solve problems like -

• Finding a path between 2 nodes in a graph
• Checking if a graph contains a cycle
• Counting the number of connected components in a graph

Breadth First Search (BFS)

Here, we explore all nodes at a depth level before moving to the next level. And the implementation is same as that for a tree. Using a queue.

function bfs(adj: number[][], node: number, visited: boolean[]) {
    const queue: number[] = [];
    queue.push(node);
    visited[node] = true;
    
    while(queue.length > 0) {
        const nodeToExplore = queue.shift();
        console.log(nodeToExplore);
        if (nodeToExplore === undefined) return;
        for (let i of adj[nodeToExplore]) {
            if (!visited[i]) {
                visited[i] = true;
                queue.push(i);
            }
        }
    }
}

You’ll find this to be the same as a tree wherein we first push all neighbors in the queue, and then explore them one by one.

So if I feed the adjacency list that we have to bfs, we’ll get -

const adjList = [[1, 2], [0, 2, 3], [0, 1, 4], [1, 4], [2, 3, 5], [4, 6], [5]];
const visited = new Array(adjList.length).fill(false);
bfs(adjList, 0, visited) // 0 1 2 3 4 5 6

Uses

It can be used to -

• Find the shortest path between 2 nodes
• Printing all nodes of a tree level by level
• Finding shortest transformation sequence of one word to another

Complexity

Time complexity of both DFS and BFS is O(V + E) wherein V is the number of vertices and E is the number of edges.

Leetcode Problems

Some leetcode problems you can solve for DFS -

1. 133 Clone Graph
2. 113 Path Sum II
3. 210 Course Schedule II

And for BFS -

1. 102 Binary Tree Level Order Traversal
2. 994 Rotting Oranges
3. 127 Word Ladder