Today, we’ll be looking at all the different ways a binary tree can be traversed.

First of all, what are binary trees ?

A binary tree is a type of data structure where each node can have maximum of 2 child nodes - a left node and a right node.

There are 4 ways in which we can traverse the Binary Tree -

1. InOrder traversal
2. PreOrder traversal
3. PostOrder traversal
4. Level Order traversal

Our own Binary Tree

Lets first create our own binary tree! The code for defining a node of our binary tree in TypeScript is really simple and straightforward.

class OurNode {
    val = 0;
    left: OurNode | null = null;
    right: OurNode | null = null;

    constructor(val: number) {
        this.val = val;
    }
}

I told you, it’s simple. We still haven’t created a tree out of it. Lets do that -

const root = new OurNode(1);
root.left = new OurNode(2);
root.right = new OurNode(3);
root.left.left = new OurNode(4);
root.left.right = new OurNode(5);
root.right.left = new OurNode(6);

I know, it can be pretty hard to visualize this tree, so here’s an image for it

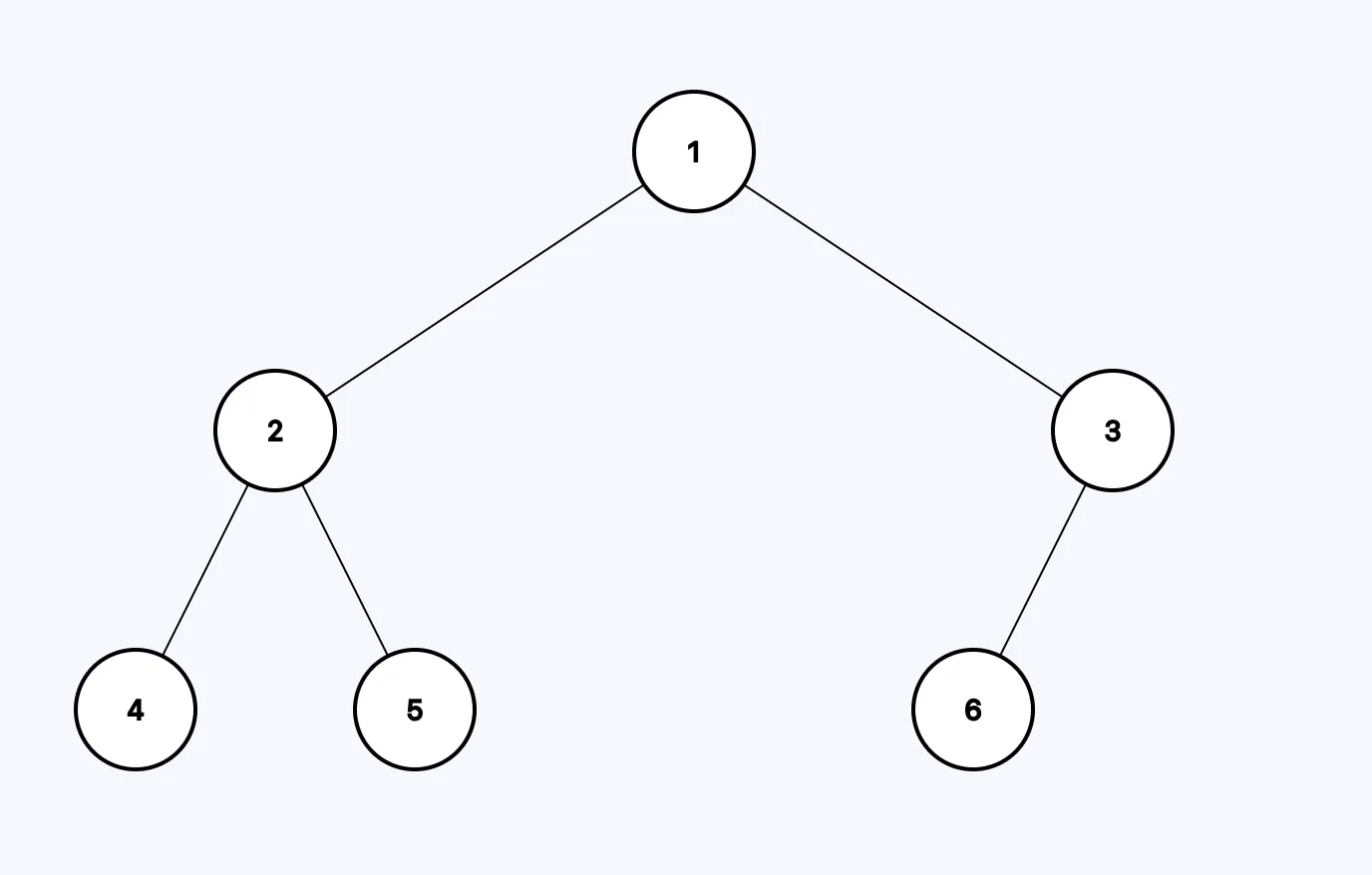
Lets talk about traversals now!

InOrder Traversal

Here, we first explore the left subtree of the node, then the node itself, and then the right subtree.

We’ll be using recursion to achieve the same.

function inOrder(node: OurNode | null) {
    if (!node) return;
    inOrder(node.left);
    console.log(node.val);
    inOrder(node.right);
}

So, if we put our own Binary tree’s root in this function,

inOrder(root);

// It will print out 4 2 5 1 6 3

PreOrder Traversal

Here, we first explore the node itself, then the left subtree, and then the right subtree.

We’ll be using recursion again to achieve the same.

function preOrder(node: OurNode | null) {
    if (!node) return;
    console.log(node.val);
    preOrder(node.left);
    preOrder(node.right);
}

So, if we put our own Binary tree’s root in this function,

preOrder(root);

// It will print out 1 2 4 5 3 6

PostOrder Traversal

Here, we first explore the left subtree, then the right subtree, and then the node itself.

We’ll be using recursion again to achieve the same.

function postOrder(node: OurNode | null) {
    if (!node) return;
    postOrder(node.left);
    postOrder(node.right);
    console.log(node.val);
}

So, if we put our own Binary tree’s root in this function,

postOrder(root);

// It will print out 4 5 2 6 3 1

Level Order Traversal

This traversal can be a bit tricky, wherein, we explore all the nodes of a level of the tree first, and then explore all the nodes in the next level of the tree.

This can be efficiently done with the help of a queue.

We start with queue having just the root in it, and then iteratively pop the first element from the left of the queue, and push its children in the queue. We do this until there aren’t any more elements left in the queue.

This algorithm is also commonly known as Breadth First Search algorithm when used in Binary Trees.

function levelOrder(node: OurNode) {
    const queue: Array<OurNode> = [];
    queue.push(node);

    while(queue.length > 0) {
        const nodeToExplore = queue.shift();
        console.log(nodeToExplore?.val);
        if (nodeToExplore?.left) queue.push(nodeToExplore.left);
        if (nodeToExplore?.right) queue.push(nodeToExplore.right);
    }
}

So, if we pass root of our own binary tree into this function,

levelOrder(root);

// this will print 1 2 3 4 5 6

Time Complexity

Time complexity of all these traversals of a binary tree is O(n), where N is the number of nodes in the tree, as each node is visited at least once.

Problems they solve

• Lets consider a Binary Search Tree wherein the left child of each node contains a value less than the node itself and the right child contains a value which is greater than the node. We can use InOrder traversal if we want to get all values of this tree in a sorted order.
• The process of serialization refers to converting a data structure into a form which can be sent as a series of bits of data which then can be deserialized and reconstructed again at the destination. We can use PreOrder traversal for this.
• Deleting a tree from the bottom can be achieved by using PostOrder traversal as child nodes or subtrees are explored first.

Leetcode Problems

Some Leetcode problems that you can solve -

• 257 Binary Tree Paths
• 230 Kth Smallest Element in a BST
• 124 Binary Tree Maximum Path Sum
• 107 Binary Tree Level Order Traversal II